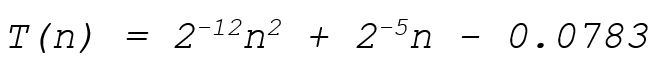BRIEF
Design an algorithm in Python that is able to take a given set of tetrominoes and assembly them into a finite target region so that they pack in the most efficient way and it is solved in the fastest time. The difficulty of this algorithm is that there are only a finite number of tetrominoes (tetris pieces) and the target region can reach sizes of up to 1000x1000.
December 2018
a 10x10 target region, solved with a 90% accuracy
SKILLS
coding
algorithm design
This was a solo project stretched over one term. The deliverable was only a script called main.py, which had to take specified inputs and deliver a signal output solution.
edge detection
The method I chose to place the tetris pieces was based off an edge detection algorithm using depth first search. This algorithm attempts to find the shapes around the edge of the polyomino target. Finding the edge shapes first lead to much more efficient algorithm, as ‘islands’ of unsolved target region were rarely left.
The algorithm first converted the target region into a neighbourhood matrix. This held the state of each square (filled or empty), and the number of neighbours that it had. A starting square was then picked, and the algorithm performed a depth first search of length four, attempting to place squares in every neighbour, but preferring to choose the squares with the fewest neighbours - this continues until a shape has been placed.
example 6x6 squares showing the placement of a neighbourhood matrix and the initial depth first searches.
divide…
The next section of the program was based on a divide and conquer algorithm. This worked by first implementing a reduction by separating the target region into a series of smaller subproblems, and then recombining them to solve. Some analysis was performed on the edge detection algorithm to work out which subproblem size gave the most accurate algorithm. It was determined that using subproblem sizes of 25x25, the most efficient initial solution could be found.
the effect of subproblem size on the algorithms accuracy…
…and on time complexity
…and conquer
Once each of the subproblems had been solved and the solutions had been recombined, some final functions were run to increase the accuracy. Several algorithms passed over the reassembled region and attempted to ‘stitch’ together the subproblem solutions by placing the remaining tetris pieces in the gaps.
example 20x20 target region, showing (from left to right) the perfect solution, the solution after initial edge detection and the solution after stitching algorithms were passed.
time analysis
To gain a better understanding of how my algorithm worked, I calculated the time complexity of the entire program. As I had used a recursive, divide and conquer algorithm, it was hoped that a time complexity of θ(n*log(n)) could be achieved. However, the additional functions that the program ran to initialize and finalize this problem unfortunately had time complexities of Ω(𝑛^2). This meant that the time complexity is dominated by the root of the problem, giving a final time complexity of: T(n) = 𝑂(𝑛^2).
graphical representation of the recursive tree used in this algorithm
In order to test this time complexity, I also performed a graphical analysis of the problem using data I’d collected by running the algorithm with different problem sizes. This yielded incredibly small coefficients for the complexity, a credit to the speed of the algorithm, and showed that my original analysis had been correct. It gave an actual time complexity of:
performance
My algorithm was consistently able to achieve accuracies of over 92% for target sizes from 10x10 up to 1000x1000. The solving time for the algorithm was also very competitive.